LA GEOMETRÍA es el estudio de las formas, tamaños y otras propiedades de las figuras en el espacio.
Los planos, cuadrados, esferas y otros cuerpos geométricos son ideas abstractas. Nunca podremos dibujar un cuadrado perfecto, aunque las técnicas geométricas nos permitan construir una aproximación.
Los principios de la geometría fueron establecidos por el matemático griego Euclides (330–275 a.c).
Más recientemente, la geometría ha incluido temas como la topología.
Los principios geométricos se utilizan en las composiciones artísticas, arquitectura, navegación, diseño de circuitos electrónicos y otras áreas de las matemáticas.
Muchos de los objetos que vemos han sido diseñados usando los principios de la geometría.
geometria
Tipos de geometría
EXISTEN muchas geometrías exóticas en las que las líneas paralelas se cortan, y en las que se incumplen otras verdades aparentemente obvias.
Algunas geometrías sólo consideran las propiedades específicas de figuras. La geometría proyectiva estudia las propiedades que se mantienen invariantes bajo la transformación de proyección.
Es un modelo del sistema visual humano: vemos que las vías férreas paralelas se encuentran en el horizonte ya que el espacio tridimensional se proyecta en una superficie bidimensional (la retina del ojo).
Se pueden clasificar las geometrías según los métodos que utilizan.
La diferencial estudia las figuras utilizando el cálculo, mientras que la analítica utiliza el álgebra y los sistemas de coordenadas.

La Anunciación, de Carlo Crivelli
Esta pintura del siglo XV muestra la geometría proyectiva. Líneas paralelas cortan en el punto de encuentro
Geometrías no euclídeas
HUBO ALGÚN momento en que se pensó que los cinco axiomas de Euclides de la geometría eran verdaderos de forma absoluta.
Pero en el siglo XIX, algunos matemáticos se dieron cuenta de que podían reinterpretar cuatro de los cinco axiomas y rechazar el quinto, obteniendo aún una geometría consistente. El quinto axioma afirma que existe exactamente una recta que pasa por un punto y es paralela a otra recta.
En las geometrías no euclídeas, no se considera este quinto axioma.
Puede ser que no exista esta paralela o que exista más de una. Una consecuencia es que la suma de los ángulos de un triángulo nunca es 180∘.
Un triángulo de ángulos rectos.
Este triángulo sobre la superficie de la Tierra tiene tres ángulos rectos, que suman 270∘.
Según la teoría de la relatividad, el espacio y el tiempo se curvan cerca de cuerpos densos como las estrellas.

La geometría de coordenadas
La geometría de coordenadas es un método para estudiar figuras geométricas mediante la asignación de números (llamados coordenadas) a cada punto del espacio. Una figura geométrica se estudia entonces en términos de las coordenadas numéricas de los puntos de la figura.
La geometría de coordenadas también se conoce como geometría analítica o geometría algebraica, y se utiliza para hallar áreas, volúmenes y áreas de superficies curvadas.
Coordenadas cartesianas
El tipo más común de coordenadas son las coordenadas cartesianas, nombradas en honor a René Descartes, quien fue el primero en describirlas en 1637. Las coordenadas cartesianas se miden respecto a dos líneas perpendiculares, llamadas ejes.
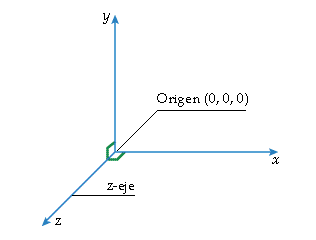
La línea horizontal se llama el eje x y la línea vertical se llama el eje y. El punto donde se cortan las dos líneas se llama origen y tiene coordenadas (0, 0).
Las coordenadas de un punto en un plano son un par de números, que normalmente se escriben entre paréntesis y separados por una coma.
El primer número indica la distancia, medida perpendicularmente, entre el punto y el eje y. Esto se puede interpretar como la distancia desde el origen medida sobre el eje x, y por ello se llama la coordenada x (o abscisa). El segundo número da la distancia desde el punto al eje x, medida perpendicularmente.
Esto también se puede interpretar como la distancia desde el origen medida sobre el eje y, y por ello se llama la coordenada y (u ordenada). Por ejemplo, el punto P en el diagrama 2 tiene las coordenadas (3, 4), donde 3 es la coordenada x y 4 es la coordenada y.
Este tipo de coordenadas se denominan coordenadas cartesianas rectangulares, porque los ejes forman un ángulo recto entre sí.
Los ejes también siguen en las direcciones opuestas desde el origen (0, 0), donde se etiquetan con números negativos.
Los ejes dividen el plano en cuatro cuadrantes. Las coordenadas de los puntos del cuadrante superior derecho son números positivos. Los puntos del cuadrante superior izquierdo tienen la coordenada y positiva, pero la coordenada x negativa.
Los puntos del cuadrante inferior derecho tienen una coordenada x positiva y una coordenada y negativa, y los puntos del cuadrante inferior izquierdo tienen coordenadas x e y negativas.
Tres dimensiones
Las coordenadas cartesianas rectangulares para designar puntos en el espacio tridimensional se obtienen añadiendo un tercer eje, llamado el eje z, que forma un ángulo recto tanto con el eje x como con el eje y. La dirección positiva del eje z es la dirección en la cual un tornillo normal avanzaría si se girara desde el eje x positivo hacia el eje y positivo.
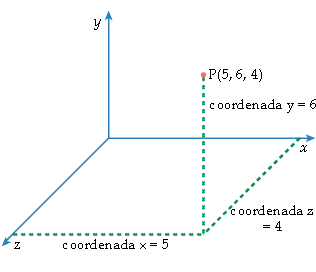
Las coordenadas de un punto en un espacio tridimensional constan de tres números, la coordenada x, la coordenada y, y la distancia al origen medida sobre el eje z, la coordenada z. Por ejemplo, el punto P del diagrama tiene las coordenadas (5, 6, 4).
Rectas y curvas
Se puede interpretar una recta o una curva como un conjunto de puntos cuyas coordenadas satisfacen una ecuación determinada, y las propiedades de la recta o de la curva se pueden deducir a partir de la ecuación utilizando el álgebra y el cálculo.
El diagrama 7 muestra un ejemplo simple de la forma en que se convierte una curva en una ecuación en coordenadas cartesianas.
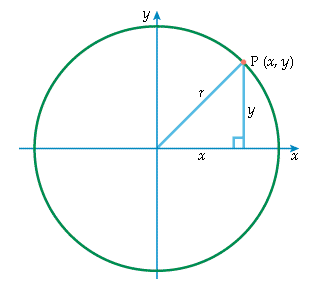
La curva es un círculo, centrado en el origen (0, 0) y con radio r.
El punto P del círculo tiene coordenadas (x, y).
Mediante el teorema de Pitágoras obtenemos la ecuación r2 = x2 + y2, aplicable a cualquier punto del círculo. Inversamente, un punto se encuentra sobre el círculo si sus coordenadas satisfacen esa ecuación. Por lo tanto, ésta es la ecuación del círculo.